Denkt man in einem künstlerischen Zusammenhang an Zeichnungen, dann sind in aller Regel Werke gemeint, die ihre Entstehung der zeichnenden Hand eines Künstlers verdanken. Die sich aus einzelnen Strichen aufbauende Zeichnung, die Linien, die als Spuren eines Stiftes auf einem Bogen Papier zurückbleiben, sind auch dann Zeichnungen, wenn der Stift nicht von einem Künstler, sondern von einer Maschine (einem Plotter) geführt wird. Es ist klar, daß dafür ein Programm notwendig ist, das konzipiert und getestet werden muß, ehe es für die Ausführung bereitsteht.
 
Der einfachste Fall einer maschinengezeichneten Linie ist der von einem definierten Punkt ausgehende gerade Strich. Verbindet man mehrere gerade Striche miteinander, entsteht ein polygonaler Linienzug. Bei der Betrachtung einer derartigen Linie erschließen sich rasch einige wichtige Eigenschaften (Parameter) für die Beschreibung (Programmierung) von beliebigen Linienzügen: Die Anzahl der Segmente, aus welchen sich der Linienzug zusammensetzt; die Winkel, die an den Knickpunkten auftreten; die relativen Längen der einzelnen Abschnitte zueinander; der Anfangswinkel gegenüber einer gedachten Achse, die Gesamtlänge des Linienzugs usw.
 
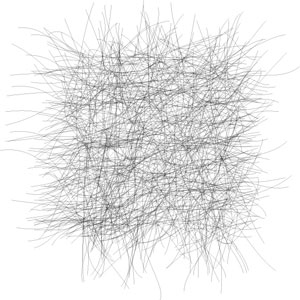
Der überwiegende Teil der auf dieser Website gezeigten Zeichnungen verwendet solche Linienzüge. Die Zeichnungen entstehen "algorithmisch", also durch ein Programm.

Die Striche zeichnende Hand erzeugt Zeichnungen in einem Universum bildnerischer Möglichkeiten – nennen wir es H-Universum. Ebenso gibt es ein Universum der durch Maschinen erzeugten Zeichnungen, ein M-Universum.
Beide haben eigene Charakteristika und beide sind unerschöpflich mächtig und reichhaltig.

Für die freie Hand gilt:


• Kein Strich gleicht dem anderen. Nur mit höchster Konzentration sind identische Striche machbar
• Auch bei einem sehr eng gefassten „Programm" für die Hand gibt es unzählige Möglichkeiten geringer Abweichungen, die in ihrer Summe für das Ergebnis bedeutend werden: die Lage des Stiftes zum Papier, die Geschwindigkeit des Ziehens, Stoßens, Reibens usw., die unterschiedlichen Andruckverhältnisse, die Mechanik und die Motorik der Hand – sie erzeugen weite Bereiche des Ausdrucks, die sich in geometrischen Beschreibungen nur schwer fassen lassen
• Die Striche zeichnende Hand arbeitet unter der Kontrolle des Auges, welches eine direkte Rückkopplung ermöglicht. Das Spektrum dieser Rückkopplung reicht von der rationalen Kontrolle über jeden Strich bis hin zur gedämpften Wahrnehmung einer Gesamtheit des Tuns und bleibt dennoch als Rückkopplung wirksam
• die Hand ermüdet

Für die zeichnende Maschine gilt:


• Sie ist unermüdlich, präzise, schnell
• Sie arbeitet mit gleichbleibender Regelmäßigkeit. Ihr zigtausendster Strich ist genau gleich wie der erste Strich
• Unregelmäßigkeiten sind materialbedingt (z. B. Risse im Papier, zu geringe Saugfähigkeit des Papiers, eingetrockneter Stift usw.)
• Auflagedruck, Ziehgeschwindigkeit und die Lage des Stiftes zum Papier sind stets gleich
• Ein Algorithmus steuert den Stift. Dieser Algorithmus wird blind abgearbeitet. Erst wenn der letzte Strich gezeichnet ist, kann das Ergebnis überprüft und bewertet werden
• Die zeichnende Maschine kann das Ergebnis selbst nicht überprüfen

Zwischen die Idee und das Ergebnis schiebt sich bei der maschinenerzeugten Zeichnung das Programm. Der "Widerstand des Materials" ist für die geplottete Linie sehr viel höher als für die mit der Hand gezeichnete Linie. Will man etwa das Thema „Von Ordnung zu Unordnung zu Ordnung" zeichnerisch darstellen, so muß man sich vergegenwärtigen, welche Veränderungen an Ordnung schließlich zu Unordnung führen können. Die Abfassung eines Programms zwingt zur Präzision und fördert Erkenntnisse über die Wirkung der eingesetzten Mittel.

Wir nehmen Magische Quadrate als ein Beispiel für einen auf mathematischen Strukturen basierenden Generator. Es handelt sich bei Magischen Quadraten um die Anordnung von Zahlen in einem quadratischen Raster derart, daß die Summe der in jeder Zeile, jeder Spalte und jeder Hauptdiagonalen stehenden Zahlen stets gleich ist. Man nennt diese Summe die magische Konstante M, und sie wird berechnet durch die Formel:

M = n (n² + 1) / 2

Bei einer Beschränkung auf Magische Quadrate mit 4 x 4 Zellen (sog. Magische Quadrate der Ordnung 4), gibt es 7040 Möglichkeiten, die Zahlen 1 bis 16 magisch anzuordnen. Geht man hypothetisch davon aus, daß die inhärente Ordnung magisch angeordneter Zahlen, wenn man eine solche sichtbar macht, sich von einer zufälligen Anordnung auch ästhetisch abhebt, kann man die mathematischen Eigenschaften der Magischen Quadrate generativ für die Erzeugung ästhetischer Ereignisse verwenden.
Ein kritischer und notwendiger Schritt dabei ist der Entwurf von Transformations-Schemata, welche die mathematische Ordnung algorithmisch in eine visuelle Ordnung überführen. Es ist eine Vielzahl solcher Transformationen denkbar; sowohl zweidimensional wie auch in höheren Dimensionen.

Die künstlerische Herausforderung ist dabei die Gedankenarbeit an der Formulierung und Programmierung konkreter Transformations-Schemata, wobei Variable wie Form, Farbe, Kontrast, Richtung, flächige oder räumliche Ausrichtung und viele mehr berücksichtigt werden können. Darauf aufbauend wird ein Programm konzipiert, welches für die algorithmische Konstruktion jeweils einzigartiger Objekt-Familien verwendbar wird. Es ist dann nicht mehr wichtig, ob der Realisierungsprozess manuell oder maschinell erfolgt.
Solche Arbeiten basieren auf der hypothetischen Annahme, daß die mathematischen Ordnungen in der Visualisierung als ästhetische Ereignisse sichtbar werden, die sich merklich von rein zufälligen Arrangements abheben.

Dabei geht es um Fragestellungen, die um algorithmisch erzeugte Kunstwerke („ästhetische Ereignisse“) kreisen.

Was sind Algorithmen, und auf welche Weise finden sie ihren Weg in die Kunst?

Ein Algorithmus ist eine präzise Anweisung zur Lösung eines mathematischen Problems, die nach endlich vielen Schritten zu einem Ergebnis führt. Benannt sind sie nach dem persischen Mathematiker Al-Khwarizmi, der vor ca. 1200 Jahren ein geometrisches Verfahren beschrieben hat, mit dem sich quadratische Gleichungen lösen lassen. Wenn man für die Lösung eines Problems einen Algorithmus kennt oder sich einen konstruieren kann, dann bedeutet dies nichts Geringeres, als dass man garantiert das Problem auch lösen kann. Das ist atemberaubend und hat als Idee Gültigkeit weit über die Mathematik hinaus. Natürlich gibt es jede Menge von Problemen, die resistent gegen Algorithmen sind, aber eben auch sehr viele, die man damit bearbeiten kann. Seit wir mit Hilfe von Computern Probleme lösen, ist die Verwendung von Algorithmen explosionsartig angestiegen. Probleme sind keine Naturphänomene, wir konstruieren sie in unseren Köpfen und können uns dann auch immer fragen: Lässt sich dafür ein Algorithmus entwerfen? Und dann: Warum sollte diese Frage vor künstlerischen Problemen Halt machen? Das kann spannend und höchst unterhaltsam sein.

Zufallsprozesse und chaotische Prozesse spielen in den hier gezeigten Arbeiten eine wichtige Rolle. Der Zufall wird gesteuert und gelenkt durch überlegte künstlerische Eingriffe (siehe Video). Mathematische Strukturen, die inhärente Ordnungen enthalten, begrenzen den Zufall auf ihre Weise.

Das zentrale Thema dabei ist: Welche bildnerischen Möglichkeiten lassen sich aus „der geplotteten Linie“ schöpfen?

Die dafür verwendeten Stiftplotter, als Computer-Peripherie heute praktisch bedeutungslos und vom Markt verschwunden, waren einmal wichtige und populäre Maschinen in technischen Produktionsprozessen. Drucker und andere Geräte sind heute an ihre Stelle getreten. Plotter-Zeichnungen sind Linienzeichnungen. Eine mechanische Zeichenmaschine – der Plotter – wird von einem Computerprogramm gesteuert, und der in die Maschine eingespannte Zeichenstift bewegt sich über das Papier und zeichnet (siehe Video), fast wie eine mechanische Hand. Einfach gesagt reagiert diese „Hand“ auf drei Befehle: Stift anheben, Stift auf das Papier aufsetzen, Stift bewegen. Wenn der Befehl Stift bewegen auf die Situation Stift ist unten trifft, dann entsteht ein Strich.

Natürlich sind Plotter für technisch-industrielle und nicht für künstlerische Vorhaben entwickelt worden. Aber mit der größten Selbstverständlichkeit haben auch Künstler sofort nach ihnen gegriffen und sie, oft unter Missachtung aller vorgegebenen technischen Grenzen, für ihre Zwecke hergerichtet und verwendet.

Plotter sind bereits historische Geräte, und mit ihrem Aussterben verschwindet auch die Chance, sie künstlerisch zu nutzen. Es gibt nur noch wenige Künstler weltweit, die auf den alten Geräten weiterarbeiten. Die Faszination, welche von einer mechanisch erzeugten, programmgesteuerten, linienorientierten Zeichnung ausgeht, hat überraschenderweise – oder logischerweise – dazu geführt, dass man sich als zeitgenössischer Künstler nun solche Geräte auf einem niedrigen Komplexitätsgrad selbst zusammenlötet. Interessant dabei ist, dass die Komponenten dieser relativ primitiven Geräte allerletzter Stand der elektronischen Technik sind. Mein „Galgen-Plotter“ ist ein solches Gerät: Eine online georderte Platine, ein Rolladenkastengetriebe, Schrittmotoren und ein Servomotor, aus dem 3D-Drucker erzeugte CAD-Komponenten, und der Stift ist mit einer Schraube festgeklemmt. Die Zeichenfläche ist ca. 160 x 180 cm. Das Gerät läuft unter 12 Volt – (siehe Video).